基本元素
平面几何可以看做是由点、线、向量、多边形、圆等基础元素构成的,下面我们先来了解如何定义这些元素
点和向量
在平面直角坐标系中,点和向量都可以被表示为一个二元组 $(x, y)$,我们用两个变量就可以表示点和向量。
struct Dot{
long double x, y;
Dot(){}
Dot(long double _x, long double _y){
x = _x;
y = _y;
}
};
线
我们通常使用一个点 $p$,和一个方向向量 $v$ 来表示一条线
$$l = p + \lambda v$$
- 当 $0 \leq \lambda \leq 1$ 时,这是一条线段
- 当 $0 \leq \lambda \leq \infty$ 时,这是一条射线
- 当 $-\infty \leq \lambda \leq \infty$ 时,这是一条直线
struct Line{
Dot p, v;
Line(){}
Line(Dot _p, Dot _v){
p = _p;
v = _v;
}
};
圆
圆可以由一个点 $p$ 表示圆心,一个数 $r$ 表示半径来确定
struct Circle{
Dot p;
long double r;
Circle(){}
Circle(Dot _p, long double _r){
p = _p;
r = _r;
}
Circle(long double _x, long double _y, long double _r){
p = Dot(_x, _y);
r = _r;
}
};
多边形
多边形可以由各个顶点的坐标来确定
struct Polygon{
int n;
Dot p[MAXN];
};
浮点误差
由于计算几何使用了 double 型浮点变量来储存结果,因此浮点误差不可避免,在进行大小比较时容易出现问题。
因此我们需要设立一个 eps 作为误差允许的范围,再进行比较
const long double eps = 1e-9;
int dcmp(long double x){
if(fabs(x) < eps)
return 0;
return x < 0 ? -1 : 1;
}
调用方法也很简单,当比较 $a$ 与 $b$ 的大小时,只需要调用 dcmp(a - b) 即可,小于,等于,大于对应的返回 $-1$,$0$ 和 $1$
向量的基础运算
向量加法与减法
坐标直接相加或相减即可
Dot operator + (Dot a, Dot b){
return Dot(a.x + b.x, a.y + b.y);
}
Dot operator - (Dot a, Dot b){
return Dot(a.x - b.x, a.y - b.y);
}
数乘向量
坐标直接相乘即可
Dot operator * (Dot a, long double b){
return Dot(a.x * b, a.y * b);
}
Dot operator / (Dot a, long double b){
return Dot(a.x / b, a.y / b);
}
向量乘法
幅角相加,模长相乘
Dot operator * (Dot a, Dot b){
return Dot(a.x * b.x - a.y * b.y, a.x * b.y + a.y * b.x);
}
向量点乘
向量 $\vec a$ 点乘 向量 $\vec b$ 相当于 $\vec a$ 在 $\vec b$ 上的投影长度乘上 $\vec b$ 的模长
long double dot(Dot a, Dot b){
return a.x * b.x + a.y * b.y;
}
向量模长
向量 $\vec a$ 的模长等于 $dot(\vec a, \vec a)$ 开二次方
long double len(Dot a){
return sqrt(dot(a, a));
}
long double len2(Dot a){
return dot(a, a);
}
向量投影长度
计算 $\vec a$ 在 $\vec b$ 上的投影长度
long double shade(Dot a, Dot b){
return dot(a, b) / len(b);
}
调整一个向量的长度
将向量 $\vec a$ 的模长调整为 $b$ 相当于乘以 $b$ 是 $\vec a$ 模长的多少倍
Dot adjust(Dot a, long double b){
return a * (b / len(a));
}
向量叉乘(叉积)
向量 $\vec a$ 叉乘 向量 $\vec b$ 相当于 $\vec a$ 和 $\vec b$ 围成的平行四边形的有向面积。
$\vec a$ 与左手向的向量叉乘为正,与右手向的向量叉乘为负,与和自己相等的向量叉乘为 $0$
long double cro(Dot a, Dot b){
return a.x * b.y - a.y * b.x;
}
判断左手向与右手向
利用叉乘的性质,$\vec b$ 在 $\vec a$ 左手向返回 $0$,右手向返回 $1$
bool direct(Dot a, Dot b){
return dcmp(cro(a, b)) <= 0;
}
垂直向量
求右手向垂直向量(叉积为正,点乘为 $0$)
Dot perpendicular(Dot a){
return Dot(a.y, -a.x);
}
向量夹角
平行四边形的面积可由边 $a$ 乘边 $b$ 乘 它们的夹角 $cos( \alpha)$ 得到,求角度移项即可
long double angle(Dot a, Dot b){
return acos(dot(a, b) / len(a) / len(b));
}
向量旋转
还记得向量乘法的 幅角相加,模长相乘 吗
要将向量 $\vec a$ 旋转 $\alpha$ 角,只需要乘上一个模长为 $1$ 幅角等于 $\alpha$ 的向量
Dot angle(long double a){
return Dot(cos(a), sin(a));
}
Dot rotate(Dot a, long double b){
return a * angle(b);
}
判断线段相交
快速排斥试验
性质一 若线段 $AB$ 和 线段 $CD$ 相交,则由他们的两个端点构成的矩形一定相交。
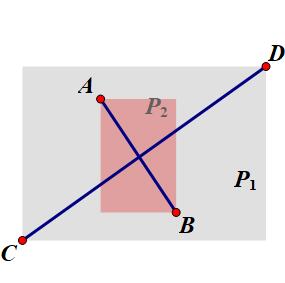
如果两条线段不满足这个性质,那么我们可以判断这两条直线不相交,如果满足,则进行跨立实验。
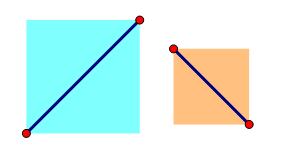
跨立试验
为什么要进行跨立实验?我们来看一种特殊的情况。
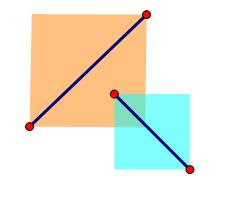
这样的线段可以通过快速排斥试验,因此我们还需要再对这种情况进行处理。
性质二 若两条直线相交,一条直线的两个端点一定在另一条直线的两侧。
这个我们可以通过之前的叉积来判断左手向和右手向,非常简单。
bool isIntersect(Line A, Line B){
Dot a = A.p;
Dot b = A.p + A.v;
Dot c = B.p;
Dot d = B.p + B.v;
if(!(max(a.x, b.x) >= min(c.x, d.x) && max(c.x, d.x) >= min(a.x, b.x) && max(a.y, b.y) >= min(c.y, d.y) && max(c.y, d.y) >= min(a.y, b.y)))
return false;
if(dcmp(cro(A.v, d-a) * cro(A.v, c-a)) <= 0 && dcmp(cro(B.v, a-c) * cro(B.v, b-c)) <= 0)
return true;
return false;
}
计算几何基本操作
计算两个点之间的距离
只需要求出两点间向量的模长即可
long double dist(Dot a, Dot b){
return len(a - b);
}
计算点到直线的距离
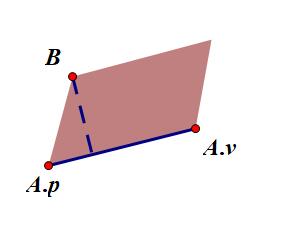
计算向量 $\overrightarrow{A.v}$ 与点 $A.p$ 到点 $B$ 的向量 构成的平行四边形的面积
$B$ 到直线 $A$ 的距离就是这个平行四边形的高,向量 $\overrightarrow{A.v}$ 就是这条高的底
long double dist(Line a, Dot b){
return fabs(cro(b - a.p, a.v) / len(a.v));
}
计算多边形面积
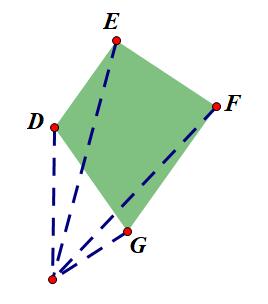
只要将多边形的顶点两两叉积,最后除以 $2$ 即可
对于图中的多边形 $DEFG$,就相当于分别计算 $ODE$,$OEF$,$OFG$,$OGD$ 的面积,因为向量叉积求得有向的,因此不在多边形内的面积会刚好被抵消(比如 $OGD$ 的面积抵消了之前三个三角形中计算的多余面积)
又因为叉积求得的面积其实是平行四边形面积,因此要除以 $2$
long double area(Polygon a){
long double ans = 0;
a.p[a.n] = a.p[0];
for(register int i=0; i<a.n; i++){
ans += cro(a.p[i], a.p[i+1]);
}
return fabs(ans / 2);
}
计算两直线交点
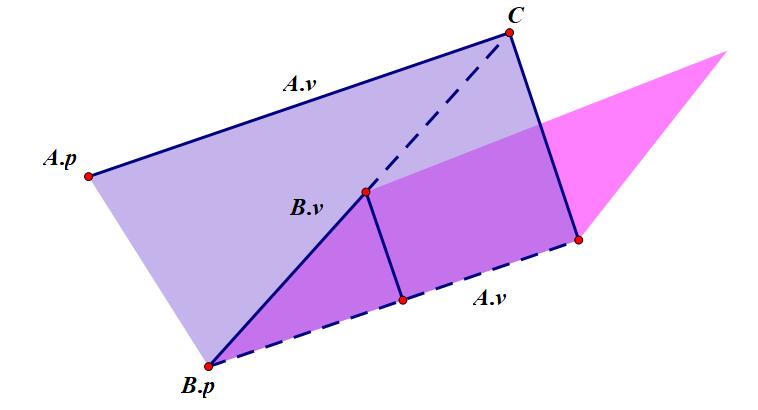
要求直线 $A$ 与直线 $B$ 的交点 $C$,只需要将点 $B.v$ 沿向量 $\overrightarrow{B.v}$ 方向平移一段距离 $x$ 即可
平行向量大小相等,因此可以将向量 $\overrightarrow{A.v}$ 平移到以 $B.p$ 为起点
我们构造两个平行四边形,一个是由向量 $\overrightarrow{A.v}$ 和 向量 $\overrightarrow{B.v}$ 构成的粉红色四边形,一个是由向量 $\overrightarrow{A.v}$ 和从 $B.p$ 到 $A.p$ 的向量构成的紫色三角形。
这两个平行四边形共底( $A.v$ ),则他们的面积之比就是高之比,因为两个三角形相似,所以高之比就是要平移的距离 $x$ 与 $\overrightarrow{B.v}$ 的模长之比
Dot intersect(Line a, Line b){
return b.p + b.v * (cro(a.v, a.p - b.p) / cro(a.v, b.v));
}
线的平移
将线 $a$ 向右手向平移 $b$ 的单位长度
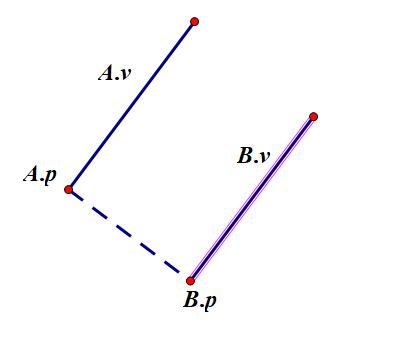
只需要构造一个与 $\overrightarrow{A.v}$ 垂直的向量,并将这个向量的长度调整至 $b$,然后将 $A.p$ 沿这个向量平移到 $B.p$,再与向量 $\overrightarrow{A.v}$ 重新组成直线即可
Line translate(Line a, long double b){
return Line(a.p + adjust(perpendicular(a.v), b), a.v);
}
点的对称
将点 $a$ 沿直线 $b$ 作对称变换
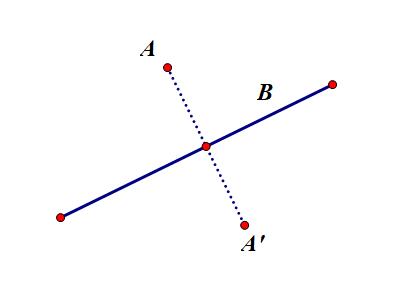
先构造经过点 $A$ 且与 $\overrightarrow{B.v}$ 垂直的向量(对应着直线 $\overrightarrow{AA’}$),求出他们的交点,再通过中点坐标公式即可得到结果。
Dot mirror(Line a, Dot b){
return (intersect(a, Line(b, perpendicular(a.v))) * (long double)2) - b;
}
线的反射
计算直线 $A$ 在直线 $B$ 上反射后的直线
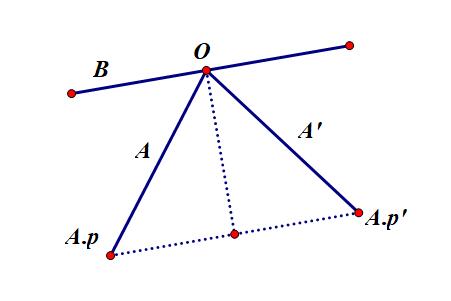
先计算出直线 $A$ 与 直线 $B$ 的交点 $O$,再构造一条过点 $O$ 且方向向量与 $\overrightarrow{B.v}$ 垂直的直线,将 $A.p$ 沿该直线对称得到 $A.p’$,过 $O$ 与 $A.p’$ 的直线即为所求
Line reflect(Line a, Line b){
Dot c = intersect(a, b);
Dot d = mirror(Line(c, perpendicular(b.v)), a.p);
return Line(c, d-c);
}
圆的交点
计算圆 $A$ 和 圆 $B$ 的两个交点
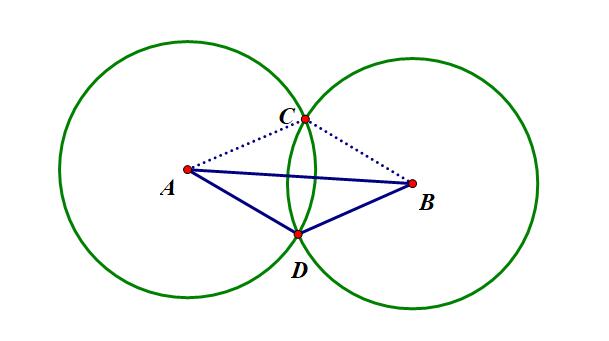
第一步,先要判断圆 $A$ 和 圆 $B$ 是否相交(不能是内含或是外离)
第二步,通过余弦定理计算出角 $CAB$ 的大小,将向量 $\overrightarrow{AB.v}$ 旋转,并调整长度为圆 $A$ 的半径长度,可以得到直线 $AC$ 与 直线 $AD$
bool circle_intersect(Circle a, Circle b, Dot &c, Dot &d){
Dot q = a.p - b.p;
long double length_2 = len2(q);
long double length = len(q);
if(dcmp(length - a.r - b.r) > 0 || dcmp(length - fabs(a.r - b.r)) < 0)
return 0;
long double aph = acos((a.r * a.r + length_2 - b.r * b.r) / (a.r * length * 2));
c = a.p + adjust(rotate(q, aph), a.r);
d = a.p + adjust(rotate(q, -aph), a.r);
return 1;
}
后记
以上是计算几何的一些最基本的操作,其他更高级的算法都是基于这些操作得到。
其他计算几何相关算法:
- Pick 定理
- 扫描线
- 二维凸包
- 旋转卡壳
- 半平面交
- KD-Tree
- …
参考资料
- yL@897982078 – 计算几何基础知识Ver2.0
- OI Wiki – 二维计算几何基础
- xia842655187 – 线段相交判断

